2026: Atualização Anual da Taxa Segura de Retirada no Brasil
Nos últimos anos, a comunidade FIRE (Financial Independence, Retire Early) vem acompanhando a evolução da Taxa Segura de Retirada (TSR) no Brasil aqui no AA40— um indicador que, em países como os EUA, serve como referência para planejamentos de aposentadoria eficiente sem esgotar o patrimônio ao longo do tempo.
Recapitulando a TSR no Brasil
Em 2025, tivemos a primeira TSR “oficial” calculada para o Brasil com base no comportamento do mercado desde 1995 até 2024 — completando 30 anos de dados completos no Plano Real. Essa TSR é uma adaptação da famosa regra dos 4% usada nos EUA, mas considerando as características dos mercados brasileiro de renda fixa e variável.
Os principais números da TSR e da Taxa Perpétua de Retirada (PWR) encontrados nesse estudo foram:
| Carteira (1995-2024) | TSR SafeMax (R$ 1 depois 30 anos) | PWR (Preservando principal) |
|---|---|---|
| 100% IBOV | 7,29% | 5,45% |
| 50% IBOV / 50% CDI-Selic | 8,48% | 6,93% |
| 100% CDI-Selic | 9,34% | 8,00% |
Dessa forma, a primeira TSR oficial do Brasil foi de 8,48% baseada na combinação 50/50 Ibovespa + CDI/Selic, que é mais ou menos a alocação que Bill Bengen utilizou nos EUA para calcular a sua.
⚠️ Importante: mesmo com resultados elevados, ainda não podemos considerar esta TSR estatisticamente robusta como uma “regra definitiva”. Ou seja, não significa que 8,48% seja seguro — apenas que, historicamente, foi essa a taxa calculada para aquele ÚNICO período de 30 anos.
2026: Atualização Anual da Taxa Segura de Retirada no Brasil
Agora, em janeiro de 2026, incorporando os dados de 2025 e mantendo o mesmo horizonte de 30 anos — temos então duas séries históricas de 30 anos: de 1995 a 2024 e de 1996 a 2025.Embora essas janelas sejam sobrepostas e pertençam ao mesmo regime monetário, elas já permitem uma análise marginalmente mais robusta do que uma única observação histórica. Porém elas são altamente correlacionadas, juros estruturalmente altos, poucos dados, ou seja, melhorou mas não tanto assim.
O objetivo continua o mesmo: responder à pergunta central do movimento FIRE no Brasil:
Quanto eu poderia ter sacado por ano, corrigido pela inflação, sem quebrar?
A Metodologia continua a mesma: Patrimônio inicial: R$ 1.000.000; Início da aposentadoria: 1995 e agora 1996. Saque inicial de x% corrigidos anualmente pela inflação (IPCA). Testamos 3 carteiras: 100% Ibovespa; 50% Ibovespa / 50% Selic; 100% Selic.
Dados de 2025:
- Ibovespa: +33,95% (ótimo desempenho)
- CDI/Selic Médio: 14,5% (juros continuam muito altos)
- IPCA: 4,26% (Inflação caiu bastante, juros reais estão bem altos)
Com estes números então já podemos concluir que a TSR do segundo período de 30 anos foi maior que o primeiro.Isto já nos permite concluir que a TSR não vai mudar, afinal, é sempre a menor de todos os períodos testados.
Para o período de 1996 a 2025:
| 100% IBOV | 50% IBOV / 50% SELIC | 100% SELIC/CDI | |
|---|---|---|---|
| TSR | 9,71% | 9,29% | 8,91% |
| PWR | 8,17% | 7,84% | 7,56% |
A TSR do período #2 (9,29%) foi acima do período #1 (8,48%), portanto a TSR Brasileira continua sendo 8,48% !
O Risco da Sequência de Retornos
Jamais podemos esquecer do SORR. Um dos maiores inimigos FIRE não é a média dos retornos, mas a ordem em que esses retornos acontecem. Esse fenômeno é conhecido como Risco da Sequência de Retornos (Sequence of Returns Risk - SORR).
Quando estamos acumulando patrimônio, a sequência pouco importa: retornos ruins no início podem até ajudar, pois permitem comprar ativos mais baratos. Já durante a fase de saque, acontece o oposto.
Retornos negativos nos primeiros anos da aposentadoria, combinados com saques constantes corrigidos pela inflação, podem causar danos irreversíveis ao portfólio — mesmo que a média de retornos ao longo de 30 anos seja boa.
É por isso que duas pessoas com o mesmo patrimônio inicial, a mesma taxa média de retorno, e a mesma taxa de retirada, podem ter destinos completamente diferentes apenas por se aposentarem em anos diferentes.
Para analisar este risco e como isto impacta a TSR, temos uma simulação chamada MONTE CARLO que é amplamenta usada não só em finanças mas como em qualquer análise de risco.
A simulação de Monte Carlo consiste em gerar milhares de trajetórias alternativas a partir da distribuição histórica de retornos observada entre 1995 e 2025. Nessas simulações, os retornos anuais são reorganizados aleatoriamente, preservando suas características estatísticas, mas criando novas sequências que nunca ocorreram na prática. Cada trajetória representa um possível “universo alternativo” para um FIRE brasileiro.
Em cada simulação, o investidor começa com um patrimônio inicial de R$ 1 milhão e realiza saques anuais corrigidos pela inflação ao longo de 30 anos, exatamente como no estudo histórico. Ao repetir esse processo milhares de vezes, é possível observar com que frequência o portfólio quebra antes do fim do período, em quais cenários ele sobrevive por pouco e em quais casos ele termina com patrimônio substancialmente maior do que o inicial em termos reais.
O valor do Monte Carlo não está em prever o futuro, mas em mapear o risco, criando as piores e melhores sequências de retorno possíveis no período. Ele mostra o quanto uma determinada taxa de retirada depende de uma sequência favorável de retornos e quão vulnerável ela é a cenários adversos logo no início da aposentadoria. Quando combinamos essa análise com a TSR histórica e com a PWR, conseguimos uma visão muito mais completa do problema: não apenas o que sobreviveu no passado, mas o quão robusta essa sobrevivência é diante da incerteza inerente ao futuro.
Em última instância, o Risco da Sequência de Retornos é o verdadeiro teste de um plano FIRE. Não basta que a estratégia funcione em média; ela precisa resistir à sequência errada no momento errado. É exatamente isso que a simulação de Monte Carlo nos ajuda a enxergar com mais clareza.
Qual a probabilidade de sucesso utilizar?
Na análise por Monte Carlo (MC), surge inevitavelmente a pergunta: qual probabilidade de sucesso é aceitável? Diferentemente da TSR histórica, que exige 100% de sobrevivência no pior período passado, o Monte Carlo trabalha com probabilidades. Não existe um número “correto” universal, mas na prática financeira costuma-se trabalhar com faixas. Probabilidades de sucesso abaixo de 80% indicam um plano frágil e excessivamente dependente de sorte na sequência de retornos. Entre 85% e 90%, o plano já se torna funcional, porém ainda vulnerável a cenários adversos prolongados. Para quem pretende viver FIRE por décadas e não tem margem para voltar ao mercado de trabalho, taxas de sucesso em torno de 95% são geralmente consideradas mais apropriadas, pois reduzem significativamente o risco de ruína mesmo diante de sequências iniciais desfavoráveis. Em outras palavras, quanto maior o horizonte e menor a flexibilidade do investidor, maior deve ser a probabilidade de sucesso exigida no Monte Carlo.
Por outro lado, buscar acima de 95% de sucesso eleva muito o custo da retirada, reduzindo desnecessariamente a renda. Probabilidades extremas protegem contra cenários extremamente raros, muitas vezes pouco realistas. Além disso, ajustes ao longo do tempo tornam 95% suficientemente seguro para a maioria dos aposentados FIRE.
Com a ajuda de AI e Python, fica mais fácil calcular estes valores hoje em dia. se quiser ver como fizemos manualmente no ano passado, clique aqui. Este é o resultado deste ano.
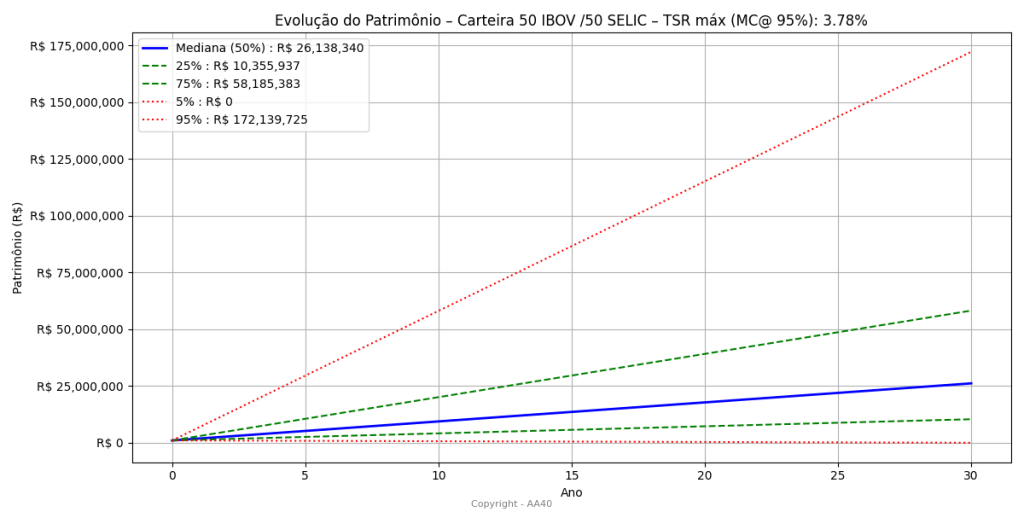
ATUALIZAÇÃO 1
Um colega, muito inteligentemente, reportou que no código Monte Carlo do resultado acima, eu estava alatorizando a inflação separadamente dos retornos do IBOV e CDI/Selic. Na vida real isto não acontece, devemos parear os dados de inflação do mesmo ano ou mês em que os retornos acontecem, e ai sim aleatorizar e sequenciar os pares. A boa notícia é que fazendo isto, a TSR Máxima segura de Monte Carlo 95% para 50%CDI/50%IBOV no Brasil sobe de 3,78% para acima de 4,5%. Boa!!!!
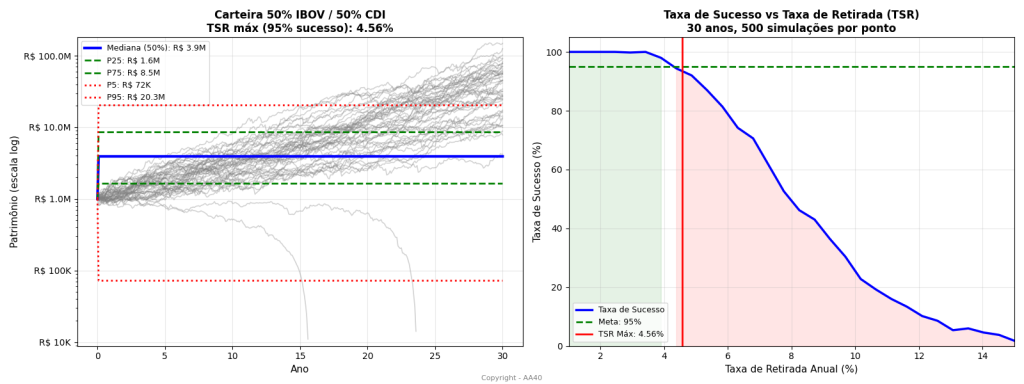
ATUALIZAÇÃO 2
Recebemos outro e-mail sugerindo que retiremos os primeiros 5 anos do Plano Real da simulação Monte Carlo, já que os juros nesse período eram muito altos e irreais. Além disso, como Monte Carlo gera sequências aleatórias suficientes, esses 5 anos iniciais não impactam tanto os resultados.
Neste meio tempo, conseguimos os dados mensais do IBOV, CDI e IPCA, o que aumentou a precisão da simulação. Em vez de trabalhar com 30 períodos (anos), agora temos 30 × 12 = 360 períodos mensais — ou 300, se excluirmos os primeiros 5 anos (1995–2000).
Com essa abordagem, atualizamos nosso simulador e rodamos novamente. A TSR Monte Carlo 95% cai consideravelmente, porque eliminamos os juros extremamente altos do início do Plano Real. Veja como fica:
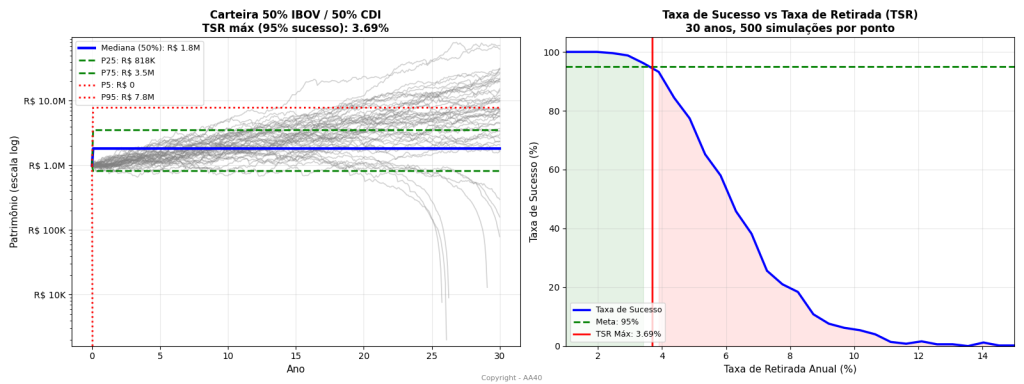
Por Curiosidade, pois muitos pedem sobre a PWR para uma carteira mais renda fixa e menos renda variável. Rodamos uma simulação de MONTE CARLO com as condições descritas no gráfico para vocês terem uma ideia.
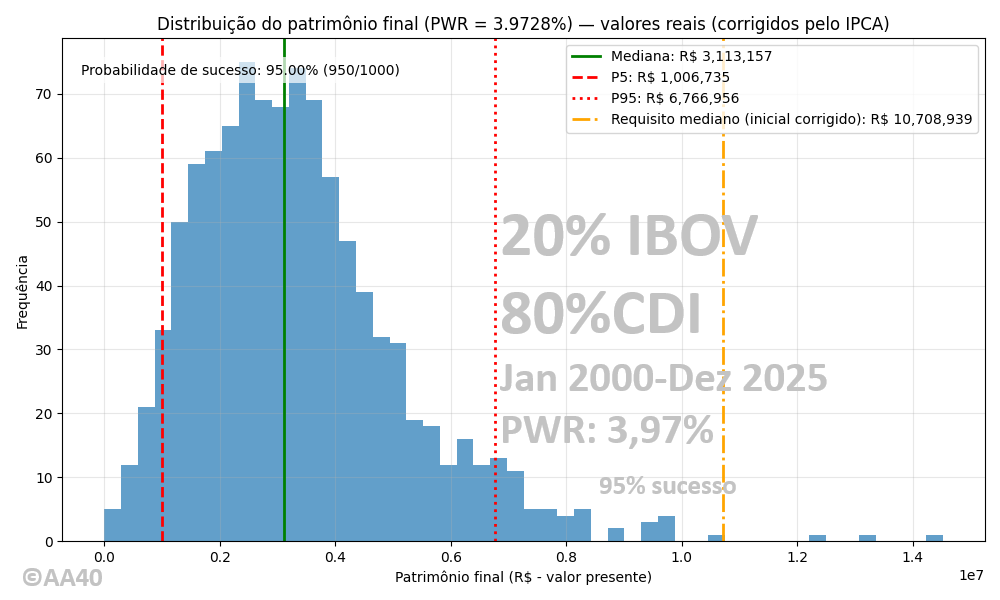
Conclusão
A incorporação dos dados de 2025 confirma que o segundo período completo de 30 anos (1996–2025) apresentou uma TSR mais alta do que o primeiro, impulsionado pelo forte desempenho do Ibovespa no último ano, juros ainda muito elevados e inflação moderada. Mesmo assim, como o método sempre adota a menor TSR entre todos os períodos testados, o valor de referência para o Brasil permanece em 8,48%, definido pelo período 1995–2024.
A nova janela histórica reforça que o ambiente brasileiro continua extremamente favorável para retiradas sustentáveis acima dos padrões internacionais, mas também evidencia a limitação estrutural da análise: poucas janelas independentes, alta correlação entre períodos e forte influência dos ciclos de juros. Ainda assim, a conclusão permanece sólida — a TSR brasileira segue em 8,48%, e nada nos dados de 2025 altera essa referência.
Embora a TSR oficial continue sendo definida pelo pior período histórico, o exercício de Monte Carlo acrescenta uma camada útil de interpretação: ele mostra como diferentes ordens possíveis dos mesmos retornos podem afetar o resultado final e evidencia a assimetria do mercado brasileiro — onde a chance de multiplicação do patrimônio é maior do que a chance de ruína quando a TSR é calibrada de forma conservadora (3,78%).
A precisão da simulação aumenta ao parear inflação e retornos em vez de aleatorizá-los separadamente, elevando a TSR máxima segura de Monte Carlo de 3,78% para acima de 4,5%. Além disso, ao remover os 5 primeiros anos do Plano Real e trabalhar com dados mensais do IBOV, CDI e IPCA, a simulação passa a ter mais janelas (até 360 períodos mensais), o que reduz o efeito dos juros excessivos iniciais e fornece uma visão mais realista da distribuição de resultados possíveis, porém a TSR cai para 3,69% a 95% e 4,14% a 90% de sucesso, ou seja, parece que 4% ainda é um bom número para usar para uma segurança bem alta.
De qualquer forma, o primeiro passo para saber o quanto você precisa e qual TSR usar é acompanhar seus gastos e seus ganhos. Faça isso no nosso remodelado e ampliado FIRE-DASH. Agora com módulo de orçamento incluso e tudo gratuito. Confira
Responda ao Questionário do Anuário FIRE 2026 - Últimos dias





Parabéns pela atualização da TSR-BR, eu estava ansioso para ver o estudo com 2 períodos, até porque estou bem no começo de uma vida como FIREE.
Quanto ao SORR, também é algo que me preocupa, mas, felizmente, estou iniciando a jornada FIRE em um ano bom em termos de taxas de retorno nos investimentos, o que já me possibilitou travar os percentuais nos primeiros anos, inclusive com boas expectativas poder revisar a minha TSR para cima no curto/médio prazo.
Obrigado pelo comentário. Bom ver que a atualização da TSR chega no momento certo para quem está começando a viver FIRE. Excelente que o SORR inicial foi favorável e que você já conseguiu travar percentuais positivos, com perspectiva de revisar a TSR para cima nos próximos anos.
A SORR é isto mesmo, assusta no início, mas passando os 10 primeiros anos, as chances das coisas darem erradas diminuem dramaticamente. Abcs
Obrigado AA40
Leio seu artigo de atualização preso no tráfego nos Alpes franceses entre megeve e val d’isere com a minha família ! Que chique !! Graças as primeiros 10 anos de vida produtiva em que poupava 90% do que ganhava , hoje em dia já estou com 4.8, independente financeiramente e cada ano mais rico com exposição baixa ao risco visto que uso 1,5% do patrimônio para os custos anuais , mas , sigo trabalhando então não gasto nada do portfólio e ainda aporto sempre algo mais ! Vida longa e feliz 2026!!
Obrigado pelo retorno! Excelente ver que disciplina e poupança nos primeiros anos rendendo frutos hoje: patrimônio crescente, gasto controlado, aporte contínuo, exposição baixa ao risco. E ainda dá para aproveitar os Alpes com a família – Nada mal! Qualidade de vida que vem do capital e da liberdade financeira. Que 2026 siga sólido, com capital trabalhando e experiências valiosas, afinal, é para isto que queremos ser FIRE. Vida longa meu caro!
Muito bom. Acho que a TSR vai tender a diminuir com o passar dos anos, pois foi necessário uma SELIC muito alta no inicio para defender o real.
Eu vou usar em 2026 uma TSR de 5,2%, mas minha TSR não é essa clássica de retirar um valor inicial e atualizar pela inflação e sim recalcular todo ano qual porcentagem do patrimônio pode ser gasta. Minha IF também leva em conta uma renda que durará 20 anos e um possível INSS pagando um SM, ou seja, minha TSR é bem particular e só serve para mim.
Belíssimo trabalho em calcular algo que sirva de uma luz guia para mais pessoas.
Abraços.
Obrigado pelo comentário. Vai cair sim, não tem como.
Excelente detalhamento da sua TSR e da abordagem personalizada. Concordo, é um trabalho que serve de referência para quem busca orientação mas cada um vai definir a sua. Abcs
Eu gostaria muito, mas não acredito que vai ter INSS daqui a 15-20 anos, nem que seja 1 SM. Eu “contribuí” pelo teto por 20 anos e acho que não vou ter 1 centavo quando bater na idade do benefício (que vai sempre aumentando). Espero estar errado.
Concordo, melhor não contar com o INSS. Se vier, será lucro, mas prudência é não depender dele.
E qual seria a taxa perpétua de retirada (pwr) brasileira pelo Monte Carlo?
Anon,
|||| AA40- Simulação de Monte Carlo para TSR Máxima |||
Configuração personalizada para a simulação de Monte Carlo
Digite a porcentagem do IBOV na carteira (0-100): 50
Digite a porcentagem do SELIC na carteira (0-100): 50
Escolha o modo de cálculo (TSR/PWR): PWR
Digite o número de anos de aposentadoria (ex.: 30): 30
Digite o valor inicial do patrimônio (ex.: 1000000): 1000000
Digite a taxa de sucesso alvo (0-100, ex.: 95): 95
Aguarde… rodando resultados…
PWR (95% de manter o patrimônio real): 1.9623%
Patrimônio final corrigido pelo IPCA (valores reais de hoje):
P5 real : R$ 1,006,609
P50 real: R$ 5,978,699
P95 real: R$ 32,547,643
Requisito mediano de preservação real (Valor Inicial corrigido por IPCA): R$ 6,746,969
Olá, no portfolio 50%/50% é feito algum rebalanceamento?
Rafael, sim, anualmente a carteira é trazida de volta a 50%/50%.
Interessante é observar que quanto mais renda fixa, maior a TSR MC, por que a volatilidade diminui muito. Porém o valor final da carteira cai. Assim como nos EUA, no início FIRE é melhor sacrificar um pouco o retorno, para aumentar a TSR segura, e depois de uns 10 anos iniciais, se aumenta novamente a renda variável. Isso é chamado de Glide path reverso. Vou escrever sobre isso em breve.
Abcs AA40
Oi AA , pensando aqui no glide path que você irá falar. Mas , você considera errado alguém que já é fire no Brasil e usa 2,5% de tsr ter aversão ao risco e manter o portfólio 90 em rf e 10 em variável . Pessoalmente o patrimônio continuará crescendo supondo selic média nos próximos anos de 9% menos 4 de inflação , 2,5 ao ano limpo de crescimento . Vc acha esse pensamento errado ???
Anon, não acho errado não: para alguém já FIRE, com TSR real de 2,5% (até poupança tem entregue isso), avesso a risco e que tlvz nunca sairá do Brasil, um portfólio 90% RF / 10% variável é coerente e tende a preservar bem e até aumentar patrimônio; tlvz 4% de inflação média é um pouco otimista, mas mesmo com inflação mais alta a estratégia continua funcionando enquanto a RF entregar prêmio real positivo, ainda mais se boa parte desta RF estiver em TD IPCA+ — o risco neste caso não é volatilidade, e sim choques estruturais (inflação fora do regime, tributação, regras), que não invalidam a alocação, apenas exigem acompanhamento contínuo.
Se quiser nos contar sua historia, entre em contato. Estamos querendo publicar artigos este ano entrevistando pessoas que já são FIRE no Brasil ([email protected]) Abcs AA40
Show! Muito obrigado pela dedicação à comunidade. Realmente é assustadora a diferença da TSR usando a simulação de MC, dá um choque de realidade sobre o que a assimetria brasileira causa. Abraço
Pois é Anô, mas dá pra mitigar isso focando mais em renda fixa. Acho que 50% 50% no Brasil é muita renda variável para quem inicia FIRE. Acumulação tudo bem, mas viver FIRE, principalmente no início dá pra ir para 80RF/20RV por uns 10 anos. Olha como fica neste caso:
|||| AA40- Simulação de Monte Carlo para TSR Máxima |||
Configuração personalizada para a simulação de Monte Carlo
Digite a porcentagem do IBOV na carteira (0-100): 20
Digite a porcentagem do SELIC na carteira (0-100): 80
Escolha o modo de cálculo (TSR/PWR): TSR
Digite o número de anos de aposentadoria (ex.: 30): 30
Digite o valor inicial do patrimônio (ex.: 1000000): 1000000
Digite a taxa de sucesso alvo (0-100, ex.: 95): 95
Aguarde… rodando resultados…
TSR máxima segura (95% de sucesso): 5.2972%
Percentis finais (R$):
P5 : R$ 0
P25 : R$ 7,981,428
P50 : R$ 16,668,353
P75 : R$ 29,337,139
P95 : R$ 60,919,811
ou para um FIRE de 40 anos
|||| AA40- Simulação de Monte Carlo para TSR Máxima |||
Configuração personalizada para a simulação de Monte Carlo
Digite a porcentagem do IBOV na carteira (0-100): 20
Digite a porcentagem do SELIC na carteira (0-100): 80
Escolha o modo de cálculo (TSR/PWR): TSR
Digite o número de anos de aposentadoria (ex.: 30): 40
Digite o valor inicial do patrimônio (ex.: 1000000): 1000000
Digite a taxa de sucesso alvo (0-100, ex.: 95): 95
Aguarde… rodando resultados…
TSR máxima segura (95% de sucesso): 4.7852%
Percentis finais (R$):
P5 : R$ 0
P25 : R$ 30,988,364
P50 : R$ 66,528,492
P75 : R$ 125,132,855
P95 : R$ 275,503,854
Bem melhor né? Abcs AA40
Eu adoro esses posts.
Ansioso pelo resultado dos próximos anos, acredito que a partir dos anos 2000 de inicio as taxas serão mais próximas das atuais.
E muito obrigado pela manutenção do site, queria ser nerd pra poder contribuir com a parte da programação, mas vou ficar devendo. kkkkkk
Abraços e que 2026 seja cheio de conquistas
Fico muito feliz em saber que você gosta dos posts — esse tipo de retorno dá sentido ao trabalho de manter o site ativo. Também concordo com você: ao olhar para os dados a partir dos anos 2000, o regime de taxas tenderá a ser mais próximo do que vivemos hoje, o que torna as análises mais relevantes para decisões atuais. E não se preocupe com a parte técnica: acompanhar, refletir, compartilhar e participar das discussões já é uma ótima forma de contribuir. Abraços e que 2026 seja, de fato, um ano de muitas conquistas para todos nós.
Gosto demais! E sempre recomendo para uns entusiastas do assunto também. Posso abusar e pedir uma simulação 70RF/30RV pra 40 anos? Que é meu plano de distribuição de patrimonio. Obrigado
Claro.
|||| AA40- Simulação de Monte Carlo para TSR Máxima |||
Configuração personalizada para a simulação de Monte Carlo
Digite a porcentagem do IBOV na carteira (0-100): 30
Digite a porcentagem do SELIC na carteira (0-100): 70
Escolha o modo de cálculo (TSR/PWR): TSR
Digite o número de anos em FIRE (ex.: 30): 40
Digite o valor inicial do patrimônio (ex.: 1000000): 1000000
Digite a taxa de sucesso alvo (0-100, ex.: 95): 95
Digite o tamanho do bloco (anos) para o bootstrap (ex.: 1 = anos independentes): 5
Aguarde… rodando resultados…
TSR máxima segura (95% de sucesso): 4.0078% (TSR) (3.14% PWR)
Percentis finais (R$):
P5 : R$ 202,918
P25 : R$ 23,020,285
P50 : R$ 60,013,988
P75 : R$ 134,885,471
P95 : R$ 412,724,867
Nada mal. 4% na mosca!
Por falar nisso, estamos patrocinando um projeto bem legal de uns colegas FIRE bem pé no chão que vcs possam ter interesse de conferir, dar sugestões e espalhar. Estamos contribuindo com a matemática da TSR/PWR pra eles. É uma espécie de Portfolio Visualizer pro Brasil. https://backtestbrasil.com/
Abcs
AA40
Olá.
Permita-me compartilhar uma ideia para diminuir o impacto do risco de sequência de retornos desfavoráveis.
Quando tiver uma data para iniciar as retiradas do portfólio (acredito que o termo seja declarar FIRE), pense em algum instrumento financeiro que funcione como annuity. O Tesouro Renda Mais ou Educa Mais são ferramentas interessantes nesse sentido.
Veja quanto teria que resgatar da sua carteira para “comprar” essa annuity, de tal maneira que o restante da carteira permita crescimento robusto.
Fixe um período para essa annuity, por exemplo 5 ou 10 anos.
Use as parcelas da annuity como salário.
Deixe o restante da carteira como se estivesse na fase de acumulação.
Depois do período escolhido repita o processo.
Não é perfeito, mas tem alta probabilidade de amenizar o risco de sequência de retornos. A parte que você está consumindo do patrimônio é renda fixa, portanto previsível. O restante da carteira passa a se comportar como uma carteira de acumulação de tal forma que ao final do período ela tenha rendido para permitir a próxima retirada para compra de outra annuity.
Se a preocupação é com a possibilidade de no prazo da annuity a carteira de acumulação apresentar desempenho desfavorável, use um prazo maior. Se ainda assim o longo prazo causar desconforto, lembremos que no longo prazo todos seremos pó, inclusive nossas carteiras de investimento.
Em tempo, parabéns pelo blog AA40. Tiro insights muito bons do conteúdo que você publica.
Abraço a todos.
Cara, muito bom esse seu plano. Colei no gemini e pedir p ele fazer uma análise. Gostei muito do resultado.
Pra quem tá em fase de fruição, vale mais a segurança do que correr riscos para obter retornos expressivos. Precisamos cuidar do patrimônio de forma segura e tranquila para evitar a ruína, nd de emoção nessa parte da nossa vida.
Acumulamos por anos, nos arriscamos por anos, na hora da aposentadoria temos que ter previsibilidade e curtir o restante da vida numa boa.
Discordo um pouco
No IPCA+ tradicional ou IPCA+ com juros semestrais, você pode:
– vender quando quiser
– receber cupons (no JS)
– usar o dinheiro para qualquer coisa
– montar sua própria estratégia de renda
No Educa+ / Renda+, você:
– não recebe nada antes do vencimento
– não tem cupons
– não escolhe quando começa a renda (é o vencimento)
– não escolhe por quanto tempo recebe (5 anos no Educa+, 20 anos no Renda+)
Flexibilidade zero. E ainda tem imposto de renda mesmo usando pra educação ou aposentadoria? Pqp. Qual a vantagem de uma merda assim? Fosse igual os 529 nos eua ai sim mas não é. Não vale a pena nem como annuity, ipca+ é mais flexível.
Se vc não precisa do dinheiro a curtO prazo , o montante inicial rende sempre sobre o total , ao final do período se torna bem vantajoso. Creio q para quem pode esquecer parte da grana assim vale muito a pena .
Olá Rafa. Acredito que você está equivocado quanto a proposta do LB no uso do Educa+ e do Renda+ como fonte de fluxo para quem começa o usufruto do FIRE. Analisando:
“No IPCA+ tradicional ou IPCA+ com juros semestrais, você pode:
– vender quando quiser – Não é bem assim. Dependendo da marcação a mercado, você pode exaurir muito rapidamente os seus títulos IPCA+ (normal e com juros) para cobrir as suas despesas mensais e até anuais. Dê uma olhada em como a marcação a mercado dos últimos cinco anos inviabilizou a venda antecipada destes tipos de títulos, com especial atenção ao IPCA+ normal (sem juros).
– receber cupons (no JS) – Para receber cupons semestrais relevantes neste tipo de título o valor investido tem que ser relativamente alto, para alguns até impeditivo, sem falar na alocação excessiva em um único título. Exemplo real: um título IPCA+ 2040 com juros pagando R$ 10.000,00/ano (menos de R$ 1.000,00/mês) precisa ter em média R$ 180.000,00 investidos. O verdadeiro retorno deste título é no seu vencimento (geralmente em horizontes bem distantes)
– usar o dinheiro para qualquer coisa – Tanto o Educa+ quanto o Renda+ também podem ser usados em qualquer coisa (como qualquer título do TD), sendo que estes também podem ser vendidos a qualquer momento (com uma carência de 60 dias após o investimento , sujeito à marcação de mercado também).
– montar sua própria estratégia de renda – Neste caso o Educa+ traz bem mais opções para estratégias de fluxo de caixa. A “escadinha” de CDBs que investidores mais antigos faziam pode ser muito bem adaptada para “escadinha” de Educa+
No Educa+ / Renda+, você:
– não recebe nada antes do vencimento – Aqui você tem um erro conceitual. Você recebe durante todo o prazo do título (valor investido, juros e reajuste da inflação). Por exemplo, quem tem Educa+ 2026 já recebeu no dia 15/01 a primeira parcela das 60 que seram pagas até dez/30. No vencimento deste título você recebe a última parcela. No Renda+ 2030, a mesma ideia, começando em jan/30 até dez/49. Uma ideia interessante para fluxo de caixa é Educa 2027 + Renda 2030, sendo que de jan/2030 até dez/2031 você teria a sobreposição das duas rendas.
– não tem cupons – Aqui tem uma diferença de interpretação. Enquanto o IPCA+ com cupom paga duas vezes por ano, o Educa e o Renda pagam mensalmente. Lembrando que no IPCA+ com cupom o valor relevante é recebido apenas no vencimento (prazos bem grandes), com o risco de reinvestimento.
– não escolhe quando começa a renda (é o vencimento) – Escolhe sim. O Educa tem prazos que começam em 2027 até 2043 (!!!). O vencimento do titulo é quando paga a última parcela.
– não escolhe por quanto tempo recebe (5 anos no Educa+, 20 anos no Renda+) – Daí é uma questão de gosto. No meu caso, que já sou FIRE a um ano, os prazos de 5 e 20 anos de recebimento são mais do que suficientes para um planejamento robusto de fluxo de renda.
Por fim, a flexibilidade nestes tipos de título é enorme, para quem precisa de previsibilidade (essencial para quem é FIRE) e gosta de planejamento financeiro. Agora a questão do imposto, realmente deste ninguém escapa, nem se vender o IPCA+ como você sugere . Lembrando que o Educa+ é só o nome. Não precisa ser gasto exclusivamente com despesas em educação. O que não acontece com o 529 americano que deve ser usado somente com gastos de educação para ter benefício tributário.
O post ficou muito extenso, mas achei que você trouxe pontos muito equivocados que precisavam ser esclarecidos, principalmente para quem esta começando a jornada de acumular para chegar ao FIRE.
Abraços
Desculpe minha ignorancia mas Educa+/Renda+ não retornam o principal todo mês enquanto o IPCA+ c JS só o juro real e mantem o principal? Isso daria uma diferença enorme no FIRE.
Obrigado pela sua dedicação aos seus leitores. O nosso comodismo nos leva para o YouTube porém não tem nem comparação pelo que é aprendido nos blogs e em especial no AA40. Encerrei o segundo ano de vida fire com retiradas abaixo de 4% anuais com cerca de 90% em renda fixa (maioria ipca com juros semestrais) e 10% em renda variável Brasil.
Vida longa para você e seu blog.
Muito obrigado pela mensagem e pelas palavras gentis. Ficamos satisfeitos em saber que o conteúdo do blog tem sido útil, especialmente para quem já está vivendo a fase FIRE na prática. Sua disciplina — retiradas abaixo de 4% e uma alocação majoritariamente em renda fixa — é um exemplo de coerência entre objetivo, perfil de risco e contexto brasileiro. Vida longa para você nessa jornada, e seguimos em frente com o blog.